序 超伝導
超伝導現象は1911年、オランダはライデン大学のオンネス(H. K. Onnes)らによって発見された巨視的な量子現象である。
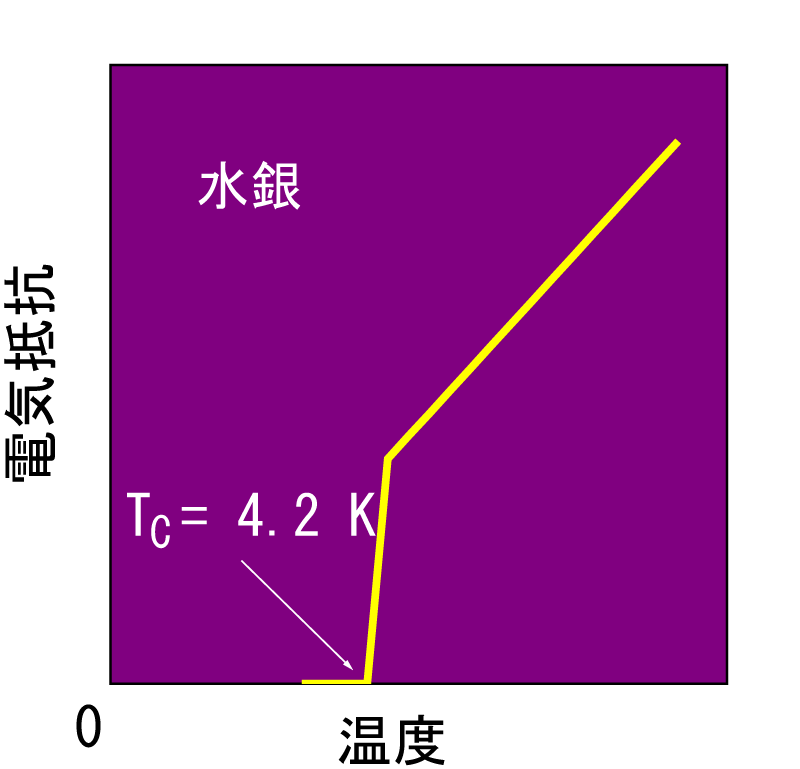 オンネスらは絶対温度4.2Kにおいて水銀の電気抵抗が消失する様子を記録した。人類が目にした新しい自然の姿であった。
超伝導体は完全反磁性 (Meissener-Ochenfeld 効果)、永久電流及び磁束の量子化、あるいは
Josephson 効果などの極めて多彩な電磁気学的性質を持った物質群である。
超伝導状態を理解する手がかりを与えたのは Bardeen-Cooper-Schrieffer (BCS) による
理論であり、ここで初めて2つの電子が対になった クーパーペアという準粒子が超伝導を
担うことが明らかになった。発見から実に40年余、1957年のことである。自然科学に携わるものとしてこういう仕事をしたいものである。
二つの電子の間に引力が働くことでそれらがクーパーペアを形成し、多数の(アボガドロ数程度の)クーパーペアが位相を揃えて
凝縮することによって超伝導は発現する。「位相を揃えて」というところが重要で、異常な電磁気学的応答の源になっている。
しばしば、クーパーペア「巨視的な位相」を獲得すると語られるが、
巨視的な数(=アボガドロ数)のクーパーペア が「同じ位相」を持つことが「巨視的」といわれる所以である。
BCS 理論は変分法に基づいて超伝導の基底状態
の記述に成功したが、その後 Bogoliubov によって「平均場」の概念が適用され超伝導の励起状態が記述
出来るようになった。これによって超伝導現象の理解は飛躍的に進んだ。量子輸送現象の研究も全て平均場の
考え方に立脚している。
オンネスらは絶対温度4.2Kにおいて水銀の電気抵抗が消失する様子を記録した。人類が目にした新しい自然の姿であった。
超伝導体は完全反磁性 (Meissener-Ochenfeld 効果)、永久電流及び磁束の量子化、あるいは
Josephson 効果などの極めて多彩な電磁気学的性質を持った物質群である。
超伝導状態を理解する手がかりを与えたのは Bardeen-Cooper-Schrieffer (BCS) による
理論であり、ここで初めて2つの電子が対になった クーパーペアという準粒子が超伝導を
担うことが明らかになった。発見から実に40年余、1957年のことである。自然科学に携わるものとしてこういう仕事をしたいものである。
二つの電子の間に引力が働くことでそれらがクーパーペアを形成し、多数の(アボガドロ数程度の)クーパーペアが位相を揃えて
凝縮することによって超伝導は発現する。「位相を揃えて」というところが重要で、異常な電磁気学的応答の源になっている。
しばしば、クーパーペア「巨視的な位相」を獲得すると語られるが、
巨視的な数(=アボガドロ数)のクーパーペア が「同じ位相」を持つことが「巨視的」といわれる所以である。
BCS 理論は変分法に基づいて超伝導の基底状態
の記述に成功したが、その後 Bogoliubov によって「平均場」の概念が適用され超伝導の励起状態が記述
出来るようになった。これによって超伝導現象の理解は飛躍的に進んだ。量子輸送現象の研究も全て平均場の
考え方に立脚している。
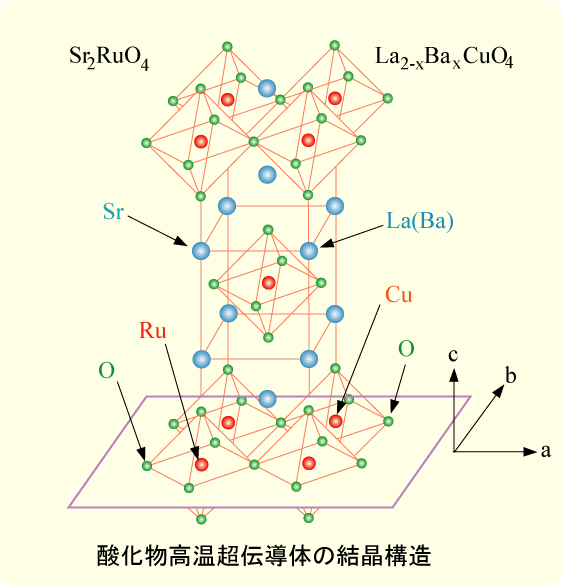 超伝導は単純な単体金属だけでなく、金属化合物や有機化合物においても発現する。
超伝導転移温度 (Tc ) は単体金属で数 K 程度であり、 Nb3Ge という化合物で 23K というのが
1980年代半ばでの記録であった。1986年スイスの J. G. Bednortz と K. A. Muller は La2-xBax
CuO4 という銅酸化物において 30K にも及ぶ高い転移温度の超伝導を発見した。この一群の超伝導体の
最大の特徴はもちろん転移温度の高さにある。
HgBaCa2Cu3Oy という銅酸化物は
135K という転移温度を記録している。しかしながらもう一つの重要な特徴は、クーパーペアの対称性が d 波対称性に
属する事である。 クーパーペアの対称性は原子軌道を分類する s、 p、 d、 f、.. という指標で分類される。
単体金属の超伝導は s 波対称性であり、重い電子系の UPt3 における超伝
導は p 波対称性に属する。
s 波以外はまとめて異方的超伝導と呼ばれている。銅酸化物超伝導体の発見以前にも UPt3 などで
発現する超伝導が異方的であることは知られていたが、これらの物質群では転移温度が 1K 以下であったため、
応用的な研究の発展する芽が無かった。一方銅酸化物超伝導体はその転移温度の異常な高さから、一種の社会現象
にまで発展し、基礎から応用研究にいたる多くの研究者がこの物質群に携わる事になった。様々な背景を持つ
多くの人が異なる方向から研究を進めると、思いもかけない不思議な現象が見出されるものである。我々が興味を持っている
異方的な超伝導体における異常な量子輸送現象も、そうした課題の一つである。
超伝導は単純な単体金属だけでなく、金属化合物や有機化合物においても発現する。
超伝導転移温度 (Tc ) は単体金属で数 K 程度であり、 Nb3Ge という化合物で 23K というのが
1980年代半ばでの記録であった。1986年スイスの J. G. Bednortz と K. A. Muller は La2-xBax
CuO4 という銅酸化物において 30K にも及ぶ高い転移温度の超伝導を発見した。この一群の超伝導体の
最大の特徴はもちろん転移温度の高さにある。
HgBaCa2Cu3Oy という銅酸化物は
135K という転移温度を記録している。しかしながらもう一つの重要な特徴は、クーパーペアの対称性が d 波対称性に
属する事である。 クーパーペアの対称性は原子軌道を分類する s、 p、 d、 f、.. という指標で分類される。
単体金属の超伝導は s 波対称性であり、重い電子系の UPt3 における超伝
導は p 波対称性に属する。
s 波以外はまとめて異方的超伝導と呼ばれている。銅酸化物超伝導体の発見以前にも UPt3 などで
発現する超伝導が異方的であることは知られていたが、これらの物質群では転移温度が 1K 以下であったため、
応用的な研究の発展する芽が無かった。一方銅酸化物超伝導体はその転移温度の異常な高さから、一種の社会現象
にまで発展し、基礎から応用研究にいたる多くの研究者がこの物質群に携わる事になった。様々な背景を持つ
多くの人が異なる方向から研究を進めると、思いもかけない不思議な現象が見出されるものである。我々が興味を持っている
異方的な超伝導体における異常な量子輸送現象も、そうした課題の一つである。
ジョセフソン効果
金属中の自由電子の状態(Fermi 液体状態も含めて)は、文字どうり自由に動き回る電子
が集まった状態である。電子に付随する「電荷」、「スピン」、「位相」
の自由度が外部からの刺激、
即ち電場や磁場、に対する応答を極めて多彩なものにしている。例えば、パーソナルコンピュータや
携帯電話のように日々利用している電子機器に含まれるデバイスの多くは、電子の電荷自由度を使って
電気信号を伝えたり、電子のスピン自由度を使って情報を記憶したりする働きをしている。
自由電子状態と比べると、超伝導や、強磁性、電荷密度波などの状態は、
何らかの秩序
を獲得した状態である。言い換えると「少し不自由」になってしまっているのだ。
強磁性ではスピン空間の回転の自由度が失われ、電荷密度波では電荷密度の並進対称性が失
われているわけである。
通常金属とこれら秩序を獲得した物質との接合系を考えたとき、秩序の種類に応じて
様々な応答(例えば電気抵抗)を示す。強磁性体の場合には磁気電気抵抗、電荷密度波の場合には
非線形電気伝導、そして超伝導の場合には電気抵抗そのものの消失といった具合である。
しかし電子の持つもう一つの大事な自由度がまだ語られていない。位相のことである。
超伝導は位相の自由度を失った秩序状態であり、
超伝導状態はその巨視的な位相によって特徴付けられる。
超伝導研究の歴史において不滅の足跡となる研究はいくつかあるが、
ジョセフソン効果の発見はその代表である。
左右の電極(超伝導体)間の電位差はゼロでも,「巨視的な位相の差」がある限り電流が発生することが1962年
Josephson によって見出された。
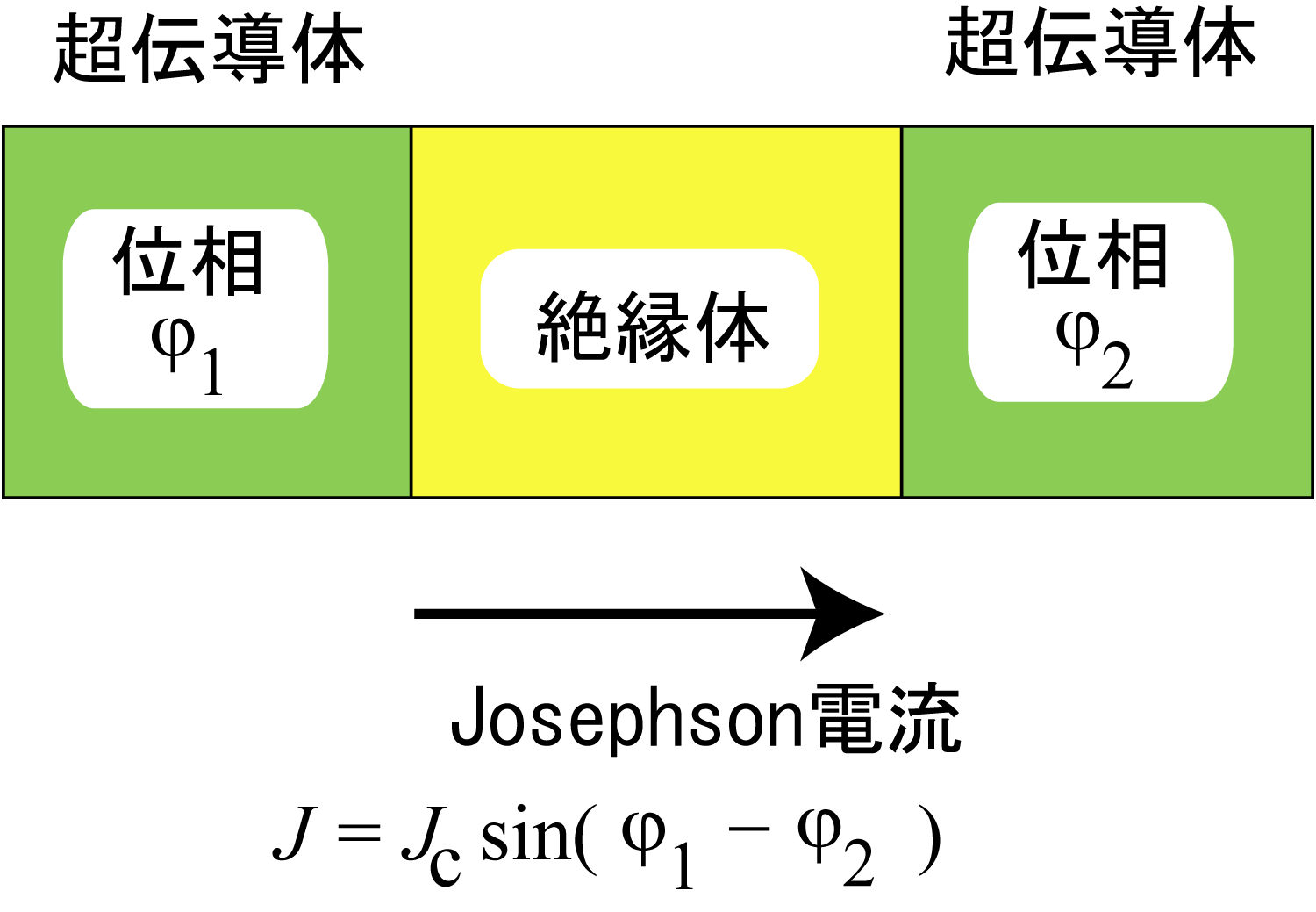
図左側の超伝導体の巨視的な
位相を φ1、薄い絶縁体を隔てた右側の
超伝導体の巨視的な位相を φ2とすると、この接合には
左右の超伝導体の位相差に応じて
J=Jc sin( φ1 -
φ2 )
という電流が流れ、この現象はジョセフソン効果と呼ばれている。Jc はジョセフソン臨界電流
と呼ばれる。
普通電流といえば系に電場を加えて平衡からずれた結果流れるもので、電子の持つ電荷
自由度が電流駆動のために直接利用されている。
しかしジョセフソン電流は電子の持つ位相の自由度を利用して駆動する電流であり、
平衡状態において流れる純粋に量子力学的電流である。
そもそも「位相」なるものが観測にかかる物理量に現れること事態が大きな驚きであった。
しかしこの事実は電磁場と電子の(クーパーペアの) 相互作用の自然な
帰結である。将に Josephson 効果は超伝導現象のハイライトである。
よく似た起源をもつ電流には
磁場中の反磁性電流や、同じく磁場中微小リングにおける永久電流などが挙げられる。
しかし、これらの電流を支えているのは時間反転対称性の破れという別の問題である。
これら電子の位相自由度に起因する電流を観測するためには、系の大きさがいわゆるメゾスコピックな
(クーパーペアがもつ位相が保たれる距離)
スケールでなくてはならない。
ジョセフソン効果はクーパーペアのトンネル効果だと理解されているが,図の絶縁体を普通の金属に置き換えても
やはり超伝導電流は流れる.普通の金属中で電流を担うのは Fermion である電子で、一方超伝導体では Boson である
クーパーペアが電流を運ぶ事になる。このように統計性を異にする粒子が 接合部
で邂逅することになる。
では接合部で何が起きているのか?その答えは アンドレーエフ反射という素過程で説明されている。
アンドレーエフ反射
我々の理論の出発点は BCS 理論である。この理論ではクーパーペアの存在を平均場という
概念を用いて記述している。そもそも超伝導は二個の電子間に引力相互作用が働く事によって発現することから、本質的には
多体問題である。平均場の導入はこの多体問題を一体問題化することを可能にする。一体 問題になってしまえばハミルトニアン
の固有値問題を解くことが容易になり、その解を基礎に超伝導体における輸送現象の理解が可能になった。通常のシュレディンガー方程式
とは異なり、我々は ボゴリューボフ=ドゥ・ジェンヌ 方程式と呼ばれる行列形式の方程式を解析的および
数値的に解くことにより、輸送現象をはじめとする様々な物理現象の機構解明を目指している。
この方程式を解くとすぐに行き当る現象が
Andreev 反射 である。図に示すのは普通の金属と超伝導体の接合である。
常伝導体中では自由電子が文字どうり自由に動き回り、その一部は超伝導体に入射しようとする。
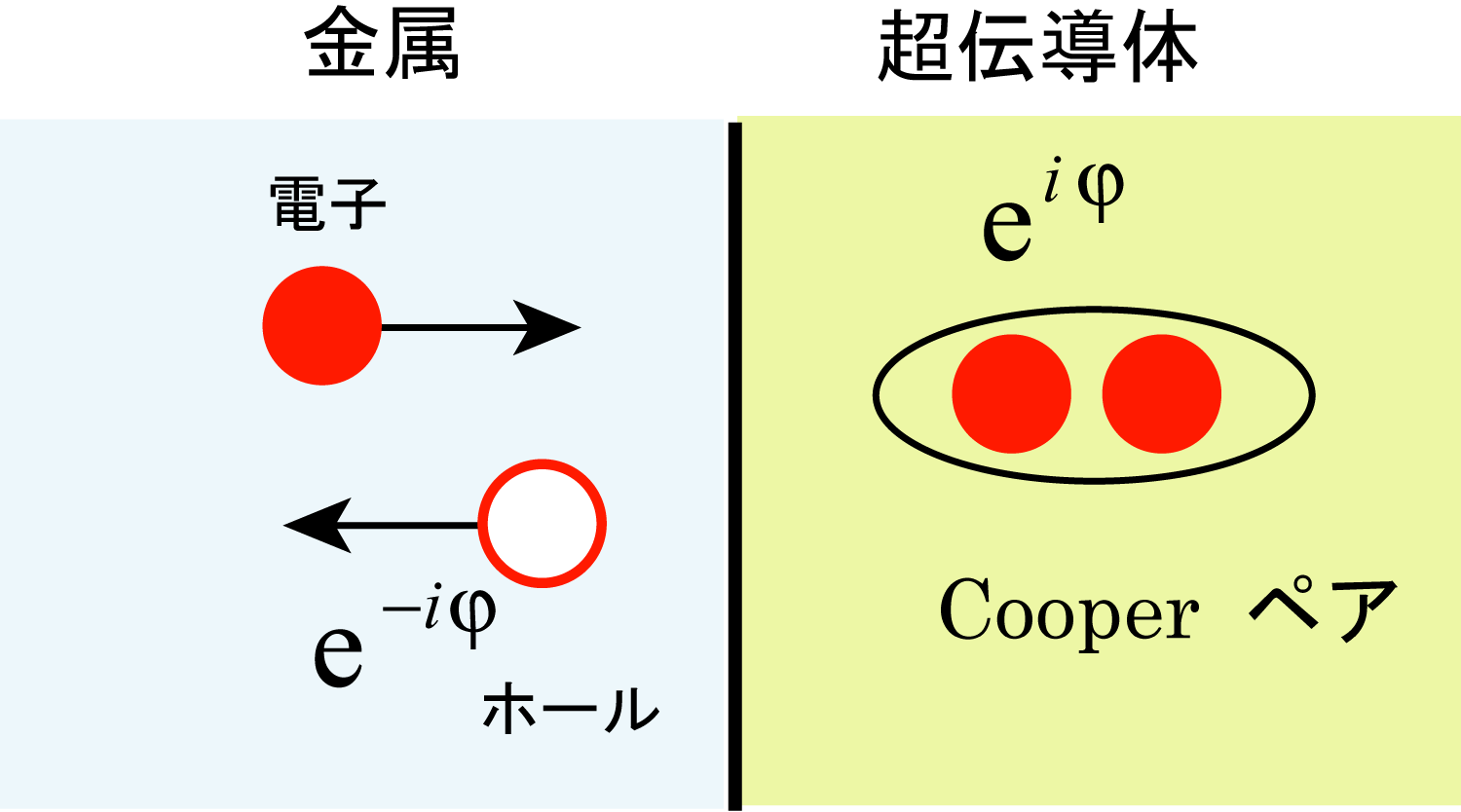
しかし超伝導体中へはクーパーペアにならない限り侵入できないのである。 クーパーペアは二個の電子と巨視的な
位相からなる複合粒子である。そこで、超伝導体に電子が入射するならば、接合近傍にいる「相方の電子」
を捕まえて、さらに巨視的位相を何処からか調達してこなければならない。このとき「相方の電子」の抜け殻として
残っている「ホール」に、調達してきた位相の複素共役な位相がコピーされて、金属側に反射される。
この現象はアンドレーエフ反射と呼ばれており、超伝導接合系の輸送現象を支配している。上述のジョセフソン電流も
ジョセフソン接合におけるアンドレーエフ反射係数を用いて記述されている。
異方的超伝導
BCS 平均場理論において、超伝導秩序を表現する秩序変数はペアポテンシャルと呼ばれ
Δs',s( r - r' ) = g( r - r' ) Fs, s'
( r - r' ),
Fs, s'
( r - r' ) =
< ψs( r )
ψs'( r' ) >
のように、電子を消滅させる演算子の積(ペアだから 2 個)の量子力学的及び統計力学的期待値としての
ペア相関関数 Fs, s' (r - r') と、二電子間に働く引力相互作用 g(r-r') の積として定義される。
ペアポテンシャルとペア相関関数は、互いに異なる物理量である。
実際に、超伝導体の表面、不純物や磁気的に活性なポテンシャルなどが、
ペアポテンシャルとは異なる対称性のペア相関を生成する場合がある。
こうしたペア相関の中で、ペアポテンシャルと同じ対称性に属するペアだけが、引力相互作用を感じてペアポテンシャルに
寄与できる。その一方で、ペアポテンシャルと異なる対称性に属するペアは、相関としてだけ存在することになる。
例えば、超伝導体に接合した金属中( g = 0 )に染み出したクーパーペアが、こうした相関の例に当たる。
異方的超伝導体では、ペアポテンシャルには寄与しないペア相関が物理現象を支配することがり、これが異方的超伝導体の
物性を豊かなものにしている。
ペアポテンシャルは一般に複素数であり、その位相部分が巨視的位相と関係している。
以下ではペアポテンシャルがペアを形成する電子の相対座標の
関数であることが大切になる。相対座標に関して Fourier 変換
Δs', s( r - r' ) = Σk
Δs',s( k ) ei k ( r - r' )
した後の Δs',s( k ) が超伝導の異方性を特徴付ける。
例えば
Δ( k ) = Δ
のように k の方向に依らない定数の場合、超伝導は s 波
と呼ばれる。通常金属の超伝導は
この s 波対称性に属する。次に
Δ( k ) = Δ kx
のような k 依存性がある場合、超伝導は p 波
と呼ばれ、 重い電子系で発現する超伝導を特徴付ける。
また、酸化物高温超伝導体は
Δ( k ) = Δ (
kx2 - ky2 )
のような d 波対称性のペアによって記述されている。
超伝導の対称性は水素原子の電子軌道の指標である s、 p、 d、 f... を用いて分類される。
s 波以外はまとめて異方的超伝導と呼ばれる。
2 次元フェルミ面におけるペアポテンシャルの
様子を示したのが下図である。真中の白抜きの円はフェルミ球を表し、その外側にペアの振幅
が描かれている。
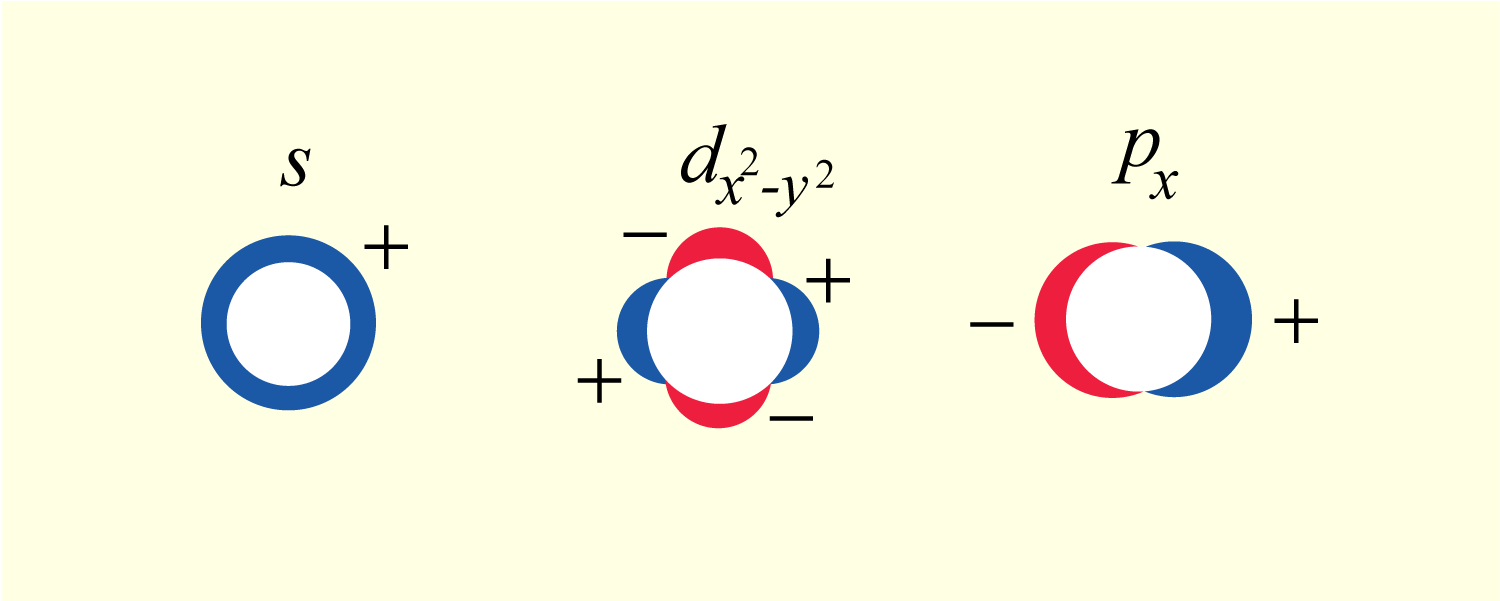
異方的超伝導の場合、すぐにわかる大切なことは フェルミ面上でペアポテンシャルの符号が変化
することである。 p 波の場合はフェルミ面上を 1 周すると 2 回、d 波の場合は 4 回符号が変わる。
e i π = -1 であることを思い起こすと、
符号の変化は π の位相変化に同じである。異方的超伝導であれば
必ず獲得することになるこの位相を内部位相と呼んでいる。この内部位相は共鳴状態の形成を
通じてアンドレーエフ反射を質的に変えてしまい、その結果ジョセフソン電流が大きく変更を受けることになる。
異方的超伝導体は 2009 年ごろからトポロジカルに非自明な超伝導体と呼ばれるようになり、
それ以前に比べて多くの研究者が関心を持つ物質群となっている。さらにトポロジカル絶縁体やトポロジカル半金属を母物質
とする超伝導体や原子層物質の超伝導体が発見されるにおよび、最近研究の対象が急速に広がっている。
異常近接効果
ペアポテンシャルの形状や符号変化に伴って、超伝導接合系の量子輸送現象は実に多彩な
変化を示す。
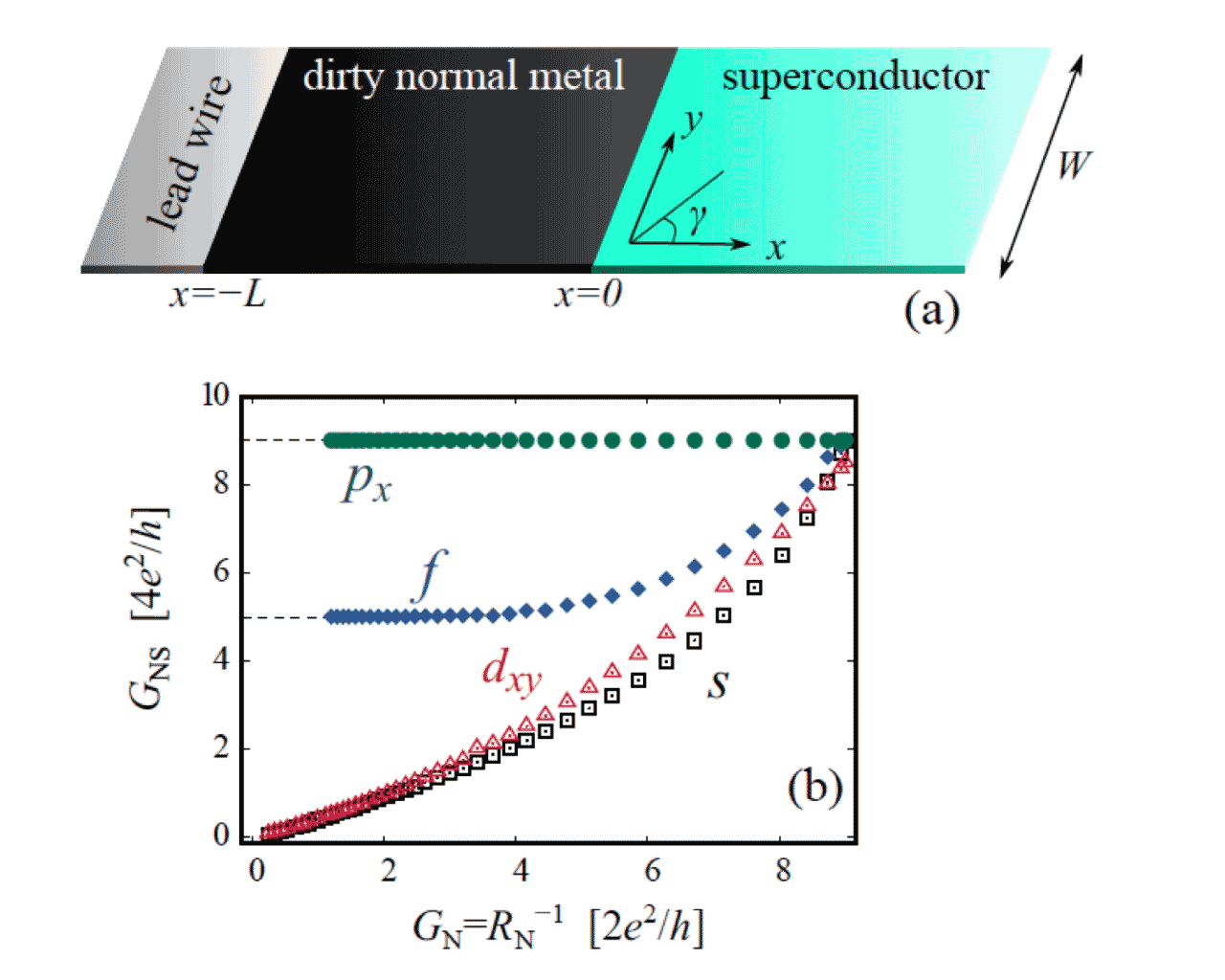 図は金属と超伝導体の NS 接合で、超伝導体がスピン三重項 p 波や f 波の場合に、異常近接効果という
奇妙な量子輸送現象を示す。
黒で塗られた金属部分にはランダムな不純物が存在し、その汚れた金属単体の
電気伝導率(コンダクタンス)GN を減らしていったとき、NS 接合の合成コンダクタンス GNS
がどうなるかを示したのが下図である。古典的にはこの接合系の合成抵抗は GNS-1
= RN + RB のように、金属の抵抗 RN = GN-1
と接合部のポテンシャル障壁の抵抗 RB の和で書けるはずである。金属の抵抗 RN を無限大に
漸近させると合成抵抗も無限大に漸近し、その結果 GNS → 0 となるはずである。実際 s 波と d 波の超伝導体
の接合では、古典的な考察が正しい。しかし、p 波や f 波の接合では、合成コンダクタンスが下げ止まり、GNS = (4e2/h) NZES に漸近していく。ここで NZES は
Atiyah-Singer の指数と呼ばれる整数である。つまりコンダクタンスが量子化しているのである。この特異な輸送現象は異常近接効果と呼ばれる。異常近接効果は元々超伝導体の表面に束縛されていたトポロジカルに守られた準粒子が、金属中に染み出しそこで
共鳴準位を形成するために起きる量子輸送現象である。Atiyah-Singer の指数は、金属中に染み出した共鳴準位の数を
表現する整数である。
この指数は、接合における波動関数を用いて定義できる位相幾何学的不変量であり、それと同時に
フェルミ準位を固有値とする微分方程式の解として得られた波動関数を用いて定義できるカイラリティという解析学的不変量にもなっている。
カイラル対称性と呼ばれる特殊な対称性を保つ系であることに着目すると、 NZES は完全
アンドレーエフ反射を起こす伝搬チャンネルの数に対応することも自然に理解できる。
我々は、このような数理構造が超伝導接合系の量子輸送現象の背景をなすことを示した。
まさに、波動関数が見えた瞬間であった。.
図は金属と超伝導体の NS 接合で、超伝導体がスピン三重項 p 波や f 波の場合に、異常近接効果という
奇妙な量子輸送現象を示す。
黒で塗られた金属部分にはランダムな不純物が存在し、その汚れた金属単体の
電気伝導率(コンダクタンス)GN を減らしていったとき、NS 接合の合成コンダクタンス GNS
がどうなるかを示したのが下図である。古典的にはこの接合系の合成抵抗は GNS-1
= RN + RB のように、金属の抵抗 RN = GN-1
と接合部のポテンシャル障壁の抵抗 RB の和で書けるはずである。金属の抵抗 RN を無限大に
漸近させると合成抵抗も無限大に漸近し、その結果 GNS → 0 となるはずである。実際 s 波と d 波の超伝導体
の接合では、古典的な考察が正しい。しかし、p 波や f 波の接合では、合成コンダクタンスが下げ止まり、GNS = (4e2/h) NZES に漸近していく。ここで NZES は
Atiyah-Singer の指数と呼ばれる整数である。つまりコンダクタンスが量子化しているのである。この特異な輸送現象は異常近接効果と呼ばれる。異常近接効果は元々超伝導体の表面に束縛されていたトポロジカルに守られた準粒子が、金属中に染み出しそこで
共鳴準位を形成するために起きる量子輸送現象である。Atiyah-Singer の指数は、金属中に染み出した共鳴準位の数を
表現する整数である。
この指数は、接合における波動関数を用いて定義できる位相幾何学的不変量であり、それと同時に
フェルミ準位を固有値とする微分方程式の解として得られた波動関数を用いて定義できるカイラリティという解析学的不変量にもなっている。
カイラル対称性と呼ばれる特殊な対称性を保つ系であることに着目すると、 NZES は完全
アンドレーエフ反射を起こす伝搬チャンネルの数に対応することも自然に理解できる。
我々は、このような数理構造が超伝導接合系の量子輸送現象の背景をなすことを示した。
まさに、波動関数が見えた瞬間であった。.
スピン三重項超伝導
電子がフェルミ粒子であることから、クーパーペアの存在を表すペア相関関数は2つの電子の入れ替え
演算の下で反対称である。
Fs',s( r' - r ) = - Fs,s'( r - r' )
多くの金属では、スピン・軌道相互作用が小さいので相関関数はスピン部と軌道部の関数の積で
表される。クーパーペアのスピンを入れ替えたときに相関関数が反対称になるのがスピン一重項ペアであり、このとき軌道部は
偶パリティの s 波や d 波になる。
その一方で、クーパーペアのスピンを入れ替えたときに相関関数が対称になるのがスピン三重項ペアであり、このとき軌道部は
奇パリティの p 波や f 波になる。
発見されたほとんどの超伝導体は、スピン一重項偶パリティ対称性のクラスに属する。スピン三重項超伝導体は
極めて稀であり、現在でもウラン系の化合物で発現しているとされているが、それら以外に有力な候補物質は無い。
スピン三重項クーパーペアはスピン S=1 を持っているため、磁気的に活性である。例えば二つのスピン三重項超伝導体の接合を
作ると、その間に超スピン流が流れることが知られている。
我々は、スピン三重項超伝導体を用いた接合のジョセフソン電流やジョセフソン・スピン流を表す公式を導き、
スピン三重項超伝導体が示す量子輸送現象の特徴を明らかにしてきた。
超伝導スピントロニクスと呼ばれる分野では、スピン三重項クーパーペアの性質から何かの機能を引き出す取り組みも
なされている。
スピン三重項超伝導体はその端にトポロジカルに守られた準粒子として マヨラナ粒子
を持つために、擾乱に強い量子計算を実現する系として注目される物質群である。
なので、スピン一重項超伝導体に磁場を加えたり、薄膜にしてスピン・軌道相互作用を導入したりして、人工的にスピン三重項超伝導体
を作る試みもなされている。実際に我々は、スピン一重項 d 波超伝導体にスピン軌道相互作用を導入すると、Atiyah-Singer の指数
が非自明な値をとり異常近接効果が起きることを示している。
奇周波数クーパーペア
二電子のスピン状態からスピン一重項とスピン三重項が、二電子の空間相対座標から偶パリティと奇パリティという対称性の
自由度が生じている。これらの他に相対時間の自由度から、二電子の時間の入れ替えに対して対称な偶周波数ペアと
反対称な奇周波数ペアに分かれることが1974年に Berezinskii によって指摘された。
ここで、時間の自由度は電子の運動方程式から導入される。
奇周波数ペアは異なる時間の二電子間に相関が残るという、あまりわかり易く無い代物である。
当初、奇周波数クーパーペアが超伝導秩序を担う「奇周波数超伝導」の発現が模索されたが、該当する超伝導体はなく、長らく
奇周波数クーパーペアの存在が忘れられていた。
 2001年になって、金属超伝導体に接合した強磁性金属の中
にいるのが奇周波数ペアであることが指摘されてから少しは知られるようになった。
トポロジカルに非自明な
超伝導体の表面では、奇周波数ペアがトポロジカルに守られたエッジ状態と共存することがわかるに至って、
奇周波数クーパーペアが我々は研究の対象になった。スピン
三重項超伝導体が示す異常近接効果は、
粒子としてはマヨラナ粒子が、ペアとしては奇周波数クーパー
ペアがこの劇的な量子輸送現象を支えていることがわかっている。
これは、一連の研究によって、我々が明らかにした事実である。
2001年になって、金属超伝導体に接合した強磁性金属の中
にいるのが奇周波数ペアであることが指摘されてから少しは知られるようになった。
トポロジカルに非自明な
超伝導体の表面では、奇周波数ペアがトポロジカルに守られたエッジ状態と共存することがわかるに至って、
奇周波数クーパーペアが我々は研究の対象になった。スピン
三重項超伝導体が示す異常近接効果は、
粒子としてはマヨラナ粒子が、ペアとしては奇周波数クーパー
ペアがこの劇的な量子輸送現象を支えていることがわかっている。
これは、一連の研究によって、我々が明らかにした事実である。
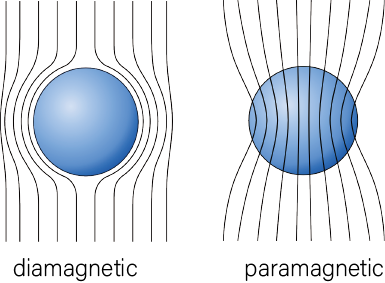
超伝導秩序を担う普通の偶周波数ペアは反磁性である。だから超伝導体は左図のようなマイスナー効果(完全反磁性)を示す。
ところが
奇周波数
クーパーペアは常磁性なのである。トポロジカル超伝導体の表面には奇周波数 Cooper ペアが局所的に存在するため、この表面も局所的に
常磁性になるのである。
このために、端や表面の割合が大きい微小なトポロジカル超伝導体は、低温で常磁性を示ことがある。
マイスナー効果はおよそ全ての超伝導体が示す現象のはずであるが、
必ずしもそうはならないという例になっている。常磁性であることは、奇周波数ペアが超伝導の位相を局所的に揺らす傾向にある、
ということである。奇周波数ペアが存在すると、位相を一様に保つのにエネルギーが必要だという見方もできる。
実際に奇周波数ペアのいるトポロジカル超伝導体の表面では、局所的に凝縮エネルギーが負
(超伝導状態の自由エネルギーが常伝導状態のそれよりも高い)になる。
さらに言い換えるならば、奇周波数ペアは超流動密度を減らす性質を持っているのである。
奇周波数クーパーペアの常磁性は、スピン三重項超伝導体の表面インピーダンスにおける異常として観測される筈だと、我々は
予測している。
 単一の伝導帯で金属状態が記述できるような単純な電子構造を持つ超伝導体では、奇周波数ペアは表面、接合界面、磁束芯、不純物の
周りなど、常に局所的に現れていた。
電子系がスピン、縮退軌道、副格子のような内部自由度を持つ場合には、奇周波数ペアが空間的に一様な基底状態の一部をなすことが最近知られるようになった。
典型的な例として、鉄系超伝導体、トポロジカルに非自明な絶縁体や半金属を母体とする超伝導体、強いスピン軌道相互作用のために電子が実質的に
合成角運動量 j=3/2 を持つような金属を母体とする超伝導体、遷移金属カルコゲナイドの薄膜超伝導体などが挙げられる。
いずれも多くの関心を集める物質群であり、こうした超伝導体に共通する性質を明らかにしようというのが最近我々が取り組ん
でいる課題である。
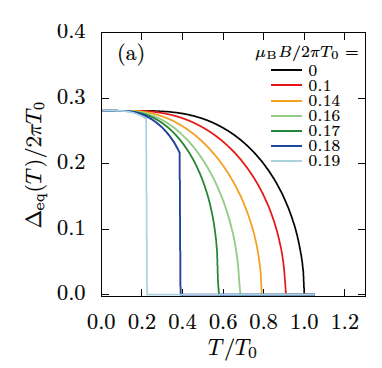
まず、空間的に一様な基底状態の一部をなす奇周波数クーパーペアも常磁性であり、奇周波数クーパーペアの存在
が超伝導を不安定化させ、その結果転移温度が下がることを明らかにした。さらに、
奇周波数クーパーペアの割合が多い超伝導相への転移は不連続になることを示した。
ゼーマン磁場中のスピン一重項 s 波超伝導体、スピン軌道相互作用の強いj=3/2 超伝導体、
軌道混成の強い2軌道超伝導体のうち異なる軌道に属する二電子が超伝導秩序を作る超伝導体などが、不連続転移を示す
超伝導体に該当する。
最初の例であるゼーマン磁場中の金属超伝導体における不連続転移は、1963年に理論的に指摘されて以来知られていた現象である。
理論研究の一方で実験的には、CeCoIn5という重い電子系の超伝導体における不連続転移の観測がなされたのが
2002年の事である。
一番の問題は、なぜ超伝導転移が不連続になるのかを、誰も満足に説明できていない点であった。
奇周波数クーパーペアが常磁性であり有限温度における超伝導ペア密度を減らす。これこそが、不連続な超伝導転移が起きる理由を
合理的に説明する唯一の物理描像であると、我々は考えている。
単一の伝導帯で金属状態が記述できるような単純な電子構造を持つ超伝導体では、奇周波数ペアは表面、接合界面、磁束芯、不純物の
周りなど、常に局所的に現れていた。
電子系がスピン、縮退軌道、副格子のような内部自由度を持つ場合には、奇周波数ペアが空間的に一様な基底状態の一部をなすことが最近知られるようになった。
典型的な例として、鉄系超伝導体、トポロジカルに非自明な絶縁体や半金属を母体とする超伝導体、強いスピン軌道相互作用のために電子が実質的に
合成角運動量 j=3/2 を持つような金属を母体とする超伝導体、遷移金属カルコゲナイドの薄膜超伝導体などが挙げられる。
いずれも多くの関心を集める物質群であり、こうした超伝導体に共通する性質を明らかにしようというのが最近我々が取り組ん
でいる課題である。
まず、空間的に一様な基底状態の一部をなす奇周波数クーパーペアも常磁性であり、奇周波数クーパーペアの存在
が超伝導を不安定化させ、その結果転移温度が下がることを明らかにした。さらに、
奇周波数クーパーペアの割合が多い超伝導相への転移は不連続になることを示した。
ゼーマン磁場中のスピン一重項 s 波超伝導体、スピン軌道相互作用の強いj=3/2 超伝導体、
軌道混成の強い2軌道超伝導体のうち異なる軌道に属する二電子が超伝導秩序を作る超伝導体などが、不連続転移を示す
超伝導体に該当する。
最初の例であるゼーマン磁場中の金属超伝導体における不連続転移は、1963年に理論的に指摘されて以来知られていた現象である。
理論研究の一方で実験的には、CeCoIn5という重い電子系の超伝導体における不連続転移の観測がなされたのが
2002年の事である。
一番の問題は、なぜ超伝導転移が不連続になるのかを、誰も満足に説明できていない点であった。
奇周波数クーパーペアが常磁性であり有限温度における超伝導ペア密度を減らす。これこそが、不連続な超伝導転移が起きる理由を
合理的に説明する唯一の物理描像であると、我々は考えている。
参考文献
入門的教科書
長岡洋介、「低温・超伝導・超流動」丸善.
長岡洋介、「極低温の世界」岩波書店
中嶋貞夫「マクロ量子現象―超伝導と超流動 物理のたねあかし」講談社サイエンティフィック
配属された卒研生に読んでもらう教科書
Y. Asano, "Andreev Reflection in Superconducting Junctions",
トポロジカル超伝導の教科書
田仲由喜夫, 「超伝導接合の物理」名古屋大学出版会
野村健太郎, 「トポロジカル絶縁体・超伝導体」丸善
古典的教科書
中嶋貞夫,「超伝導入門」培風館
A. A. Abrikosov, L. P. Gor'kov and I. E. Dzyaloshinskii, 邦訳 「統計物理学における場の量子論の方法」東京出版.
M. Tinkham, "Introduction to Superconductivity 2nd Edition", McGraw-Hill.
P. G. de Gennes, "Superconductivity in metals and alloys".
G. D. Mahan, "Many-Particle Physics", Plenum Publishers.
J. R. Schrieffer, "Theory of superconductivity", Addision Wesley.